Surprise! Orbits are never circular!
Staggering stuff I know, but really it’s remarkable that most orbits tend to be even close to circular. For the most part when making astronomical gearing we can just assume it to make things easy. After all, the complexity of introducing cyclically varying speeds is generally more trouble than it’s worth. However, for those truly daunting fabricators or those looking for very accurate designs you may need to consider some sort of correction.
But let’s back up a step and take a look at what is causing this.
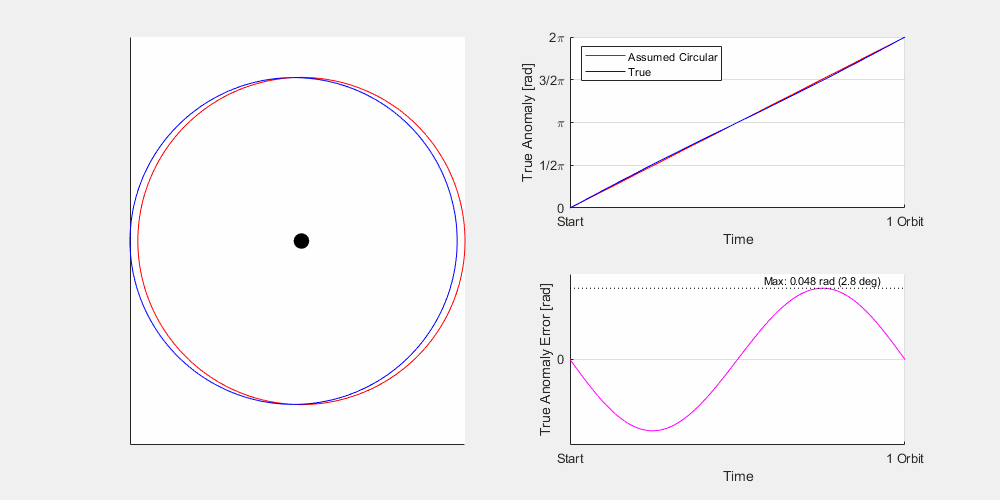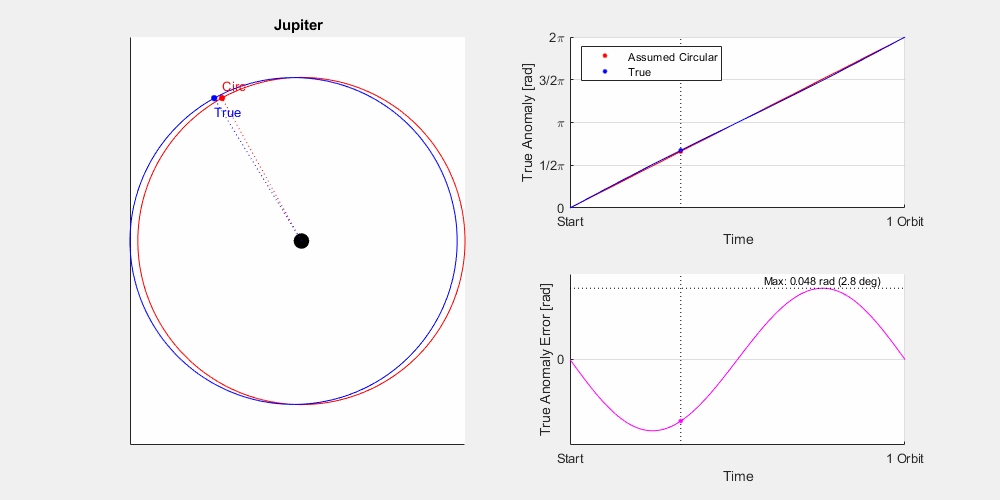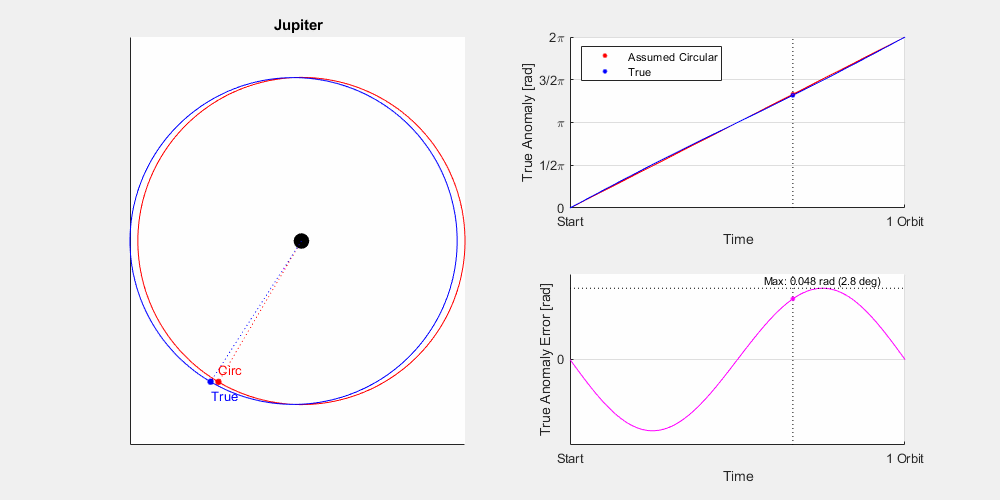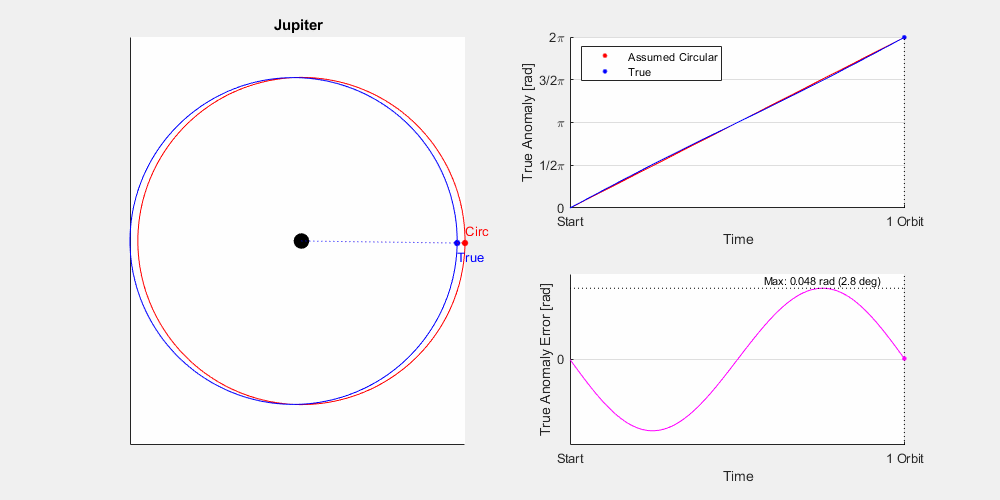
It comes down to the eccentricity (e), or how far from circular the orbit is. Let’s look at a couple moons orbiting a planet: Moon A is in a circular orbit (e = 0), and Moon B is in an elliptical orbit (0<e<1, let’s say e=0.5). They have the same overall orbital period, and you can see at two points in the animation they do line up, namely the periapsis and apoapsis. However, outside of this they vary rather significantly. Now this is a pretty extreme example but not unheard of. For example Pluto has an eccentricity of 0.248, and this will result in an error of up to 14 degrees at certain times of year. If you were hunting in the night sky for an object and were that far off you’d be hard pressed to find it. While some of Jupiter and Saturn’s moons can be pretty eccentric, most of the planets are fairly circular.
Now the you understand what’s happening, let’s take a look at some ways to correct for it
Antikythera Style Pin-Slot
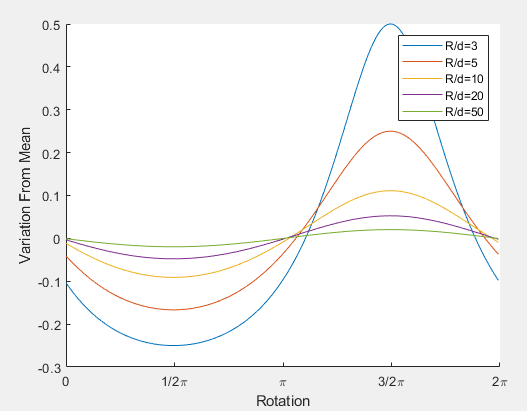
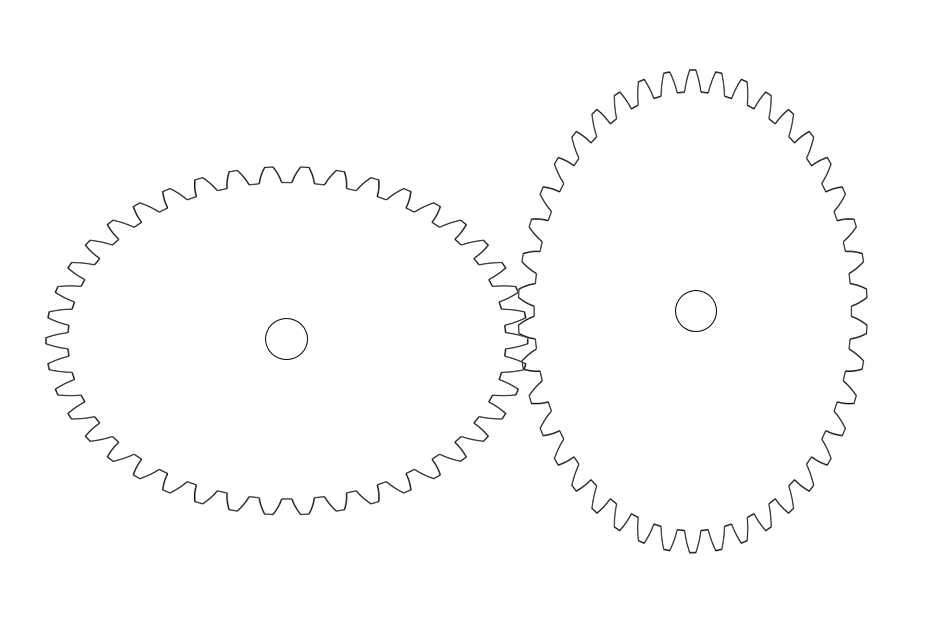
Perhaps the oldest existing method of getting this sort of non-uniform speed is the eccentric pin-slot arrangement found in the Antikythera Mechanism that has been dated to the first century BC. It’s a truly elegant solution that stacks two gear, shown in yellow and green, but rather than rotating about a common axis one is mounted eccentric to the other. One gear (the pin gear) contains a pin that mates with a slot in the other (the slot gear). The animation shows the input gear and output gear as the same size and on top of each other to illustrate the difference in the input motion and the output motion, however this would not have to be the case. The variation in speed is a result of how for out the pin is from the center of the pin gear (R), and the distance between the the rotation axes of the pin gear and slot gear (d). More specifically the ratio R/d determines how much variation is produced and how it’s distributed throughout a full rotation. If we look at a few different R/d’s below we see something similar to sinusoid, but note that high R/d’s, that is to say greatly varying speeds, become asymmetrical. Thus, this is an excellent solution for all but the most eccentric objects.
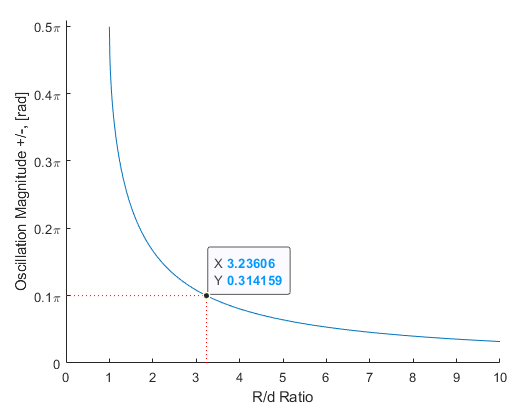
Now the relationship between the R/d ratio and the average amplitude is not trivial and would have been accomplished through trial and error for the Antikythera Mechanism. We can use modern trigonometry to define the ratio of input and output angles according to the equation below and look at the maximum and mininum of the function for each R/d to produce the curve on the right. In application, one would know the magnitude of oscillation required and use the curve to look up the R/d needed to produce that result.
Non-Circular Gearing
Another option that’s available in the modern times of CNC is non-circular gearing. You may recall that for two gears to mesh correctly the sum of their pitch radius must equal the distance between their pivots. The rule must be maintained through the entire rotation, but that doesn’t mean the pitch radius has to stay constant. A gear can have a varying radius as long as the mating gear is also varying, and inversely. While in concept this seems rather straightforward, the implementation is rather difficult. The tooth profile is now distorted and one must keep track of the clocking of the teeth relative to the clocking of the governing profile. Additionally, it is desirable that the gears be equal tooth-counts but at a minimum must be integer scales of each other.
Terms Used In This Page
Apoapsis: The highest point in the orbit, furthest from the central body. Note that this is a general term, with more specific version depending on the central body.
Apogee: Apoapsis of an orbit around Earth
Apohelion: Apoapsis of an orbit around the Sun
Apocynthion: Apoapsis of an orbit around the Moon
Eccentricity: The ‘out-of-roundness’ of the orbit. An eccentricity of 0 is a circular orbit with no apoapsis or periapsis, higher eccentricities mean a more elongated orbit.
Periapsis: The lowest point in the orbit, furthest from the central body. Note that this is a general term, with more specific version depending on the central body.
Perigee: Periapsis of an orbit around Earth
Perihelion: Periapsis of an orbit around the Sun
Pericynthion: Periapsis of an orbit around the Moon