The Equation of Time
By: Spencer Connor
What is the Equation of Time?
The Equation of Time (EoT) is the difference between apparent solar time and mean time. That’s the simplest definition, but certainly not the best for understanding the concept. So let’s make it a bit more intuitive with a narrative. For Christmas one year you received a perfectly accurate sundial and a perfectly accurate clock to run a little experiment. When your sundial reads solar noon you synchronize your clock to match and each day record the time indicated on the clock when the sundial reads noon. You will see solar noon initially occuring at 12:00, then 12:01, farther and farther after noon until mid-February where it appears at 12:15 on your clock, and then it starts getting closer to 12:00 again until it’s occurring before noon. Throughout the year this error oscillates but with variable amplitude until you are back at Christmas one year later and solar noon is back at 12:00.
If you plot this error throughout the year you will get the curve shown on the right, and it repeats itself very closely each year. This curve is what is typically referred to as the equation of time. It describes the error between a sundial (solar time) and a clock (mean time) and as such allows you to translate between the two types of time. For example, you will know in mid-October that the sun will be at its highest point at 11:45 rather than 12:00. It also allows you to read a sundial and translate to the clock time we use in modern times to an accuracy of a handful of minutes.
Why is the Equation of Time?
The EoT comes from two different effects that each cause differences between the two types of time, and when summed together the EoT curve is formed. In the image on the right the constituent curves are shown overlaid: The Effect of Eccentricity and the Effect of Obliquity
The Effect of Eccentricity
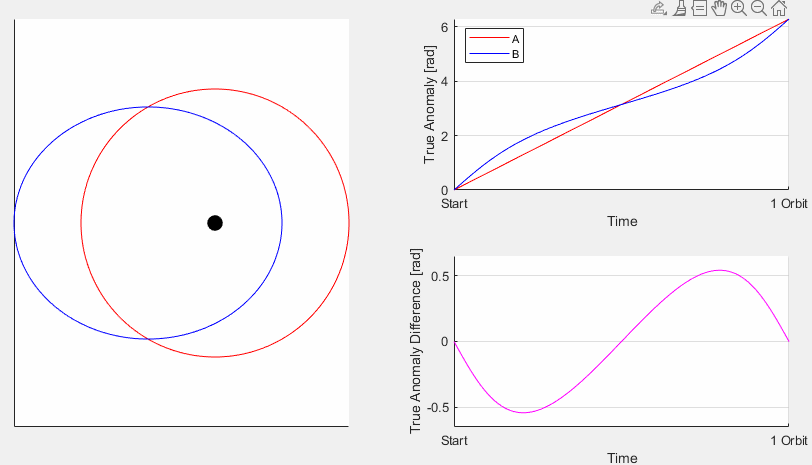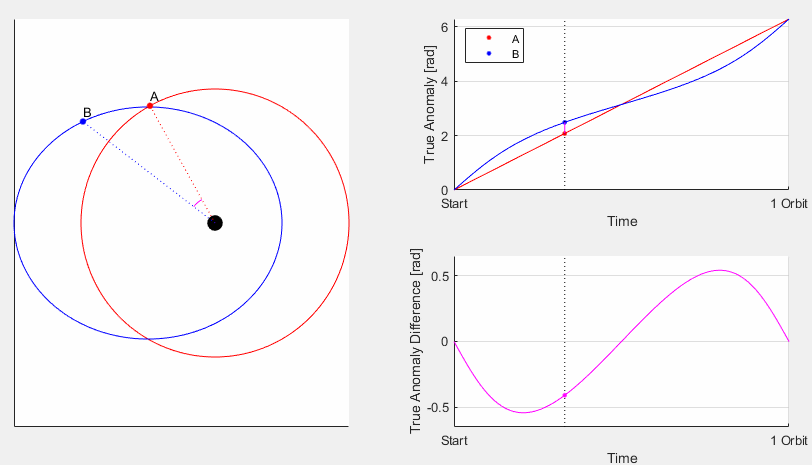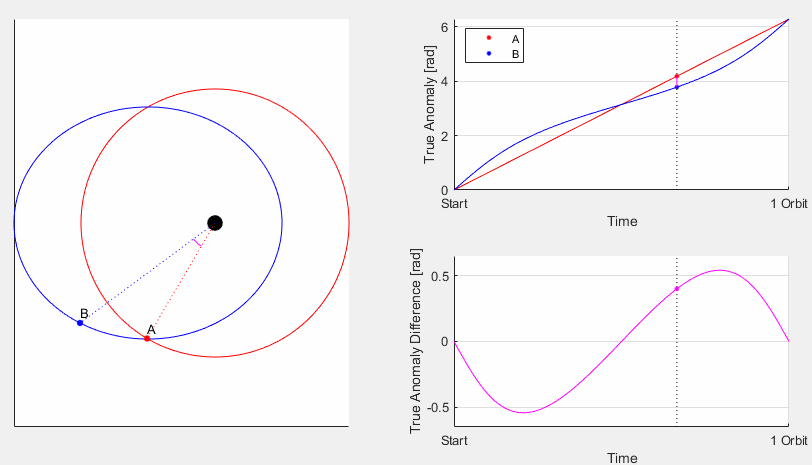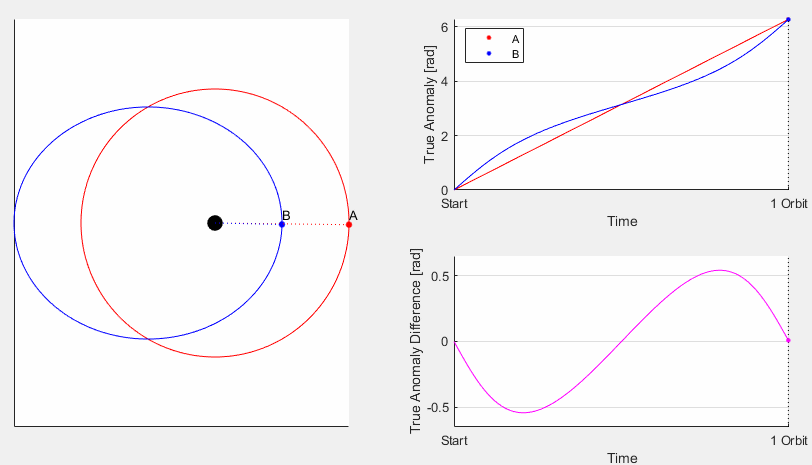
The Effect of Eccentricity comes from the orbit of the Earth around the Sun not being perfectly circular, what is referred to in orbital mechanics as its eccentricity. For Earth it is pretty low but not zero, the value is e=0.017 which translates to the distance from Earth to sun varying about ±2% through the year. Again, that doesn’t seem like much but consider that with the EoT is dealing with around 15 minutes and that isn’t very much either when there are 525,949 minutes per year. But it is actually not so much the distance directly and more the velocity that causes the effect. As stated by Kepler’s 2nd Law, orbiting objects move faster when closer to their central body so when the Earth is at its closest to the Sun (called Perihelion) it is moving faster, and therefore the sun appears to move faster. When this occurs, in early January, the sun starts getting farther and farther ahead of where it would otherwise be. The magnitude of this effect is 7.66 minutes, it has a period of one anomalistic year, and is zero at aphelion and perihelion.
Effect of Obliquity
This effect is less intuitive to visualize than the former, but is a result of the sun’s path along the celestial sphere. Since the axis of rotation of the earth is tilted (but stays roughly fixed relative to the stars) the height of the sun’s path off of the horizon (the ecliptic) varies throughout the year. The celestial sphere is mapped using right ascension, similar to longitude on earth, and declination, similar to latitude. As such, only right ascension visually changes over time as the earth rotates, while the declination remains fixed. Since the sun’s path through the sky is moving the component in the right ascension direction varies, so even if the sun moved at a constant rate the varying component in right ascension would yield a varying effect. The maximum error as a result of this effect is 9.87 minutes, it occurs with a period of half of a tropical year, and is zero at the equinoxes and solstices.
Combining The Effects for a First Order Approximation
To get the equation of time these two effects are added together to get that dual sinusoidal curve that we all know and love. Usually this is of the form EoT = 7.66*sin(2π*(t-July 5th)/365)+ 9.86*sin(2π*(t-Mar 20th)/182.5). This is a fairly good approximation and fairly easy to implement in an astronomical clock, and example is shown below. There is some odd gearing to get an arbor turning at once a year for the eccentricity component, but it’s an easy translation to twice a year for the obliquity component. Add two signal generators and a mechanical adder (menus of such contraptions) and you’re all set! Below is the implementation I used in my Antikythera Mechanism, and to the right is a conceivable design for a typical clock.
Error Analysis of First Order Mechanism
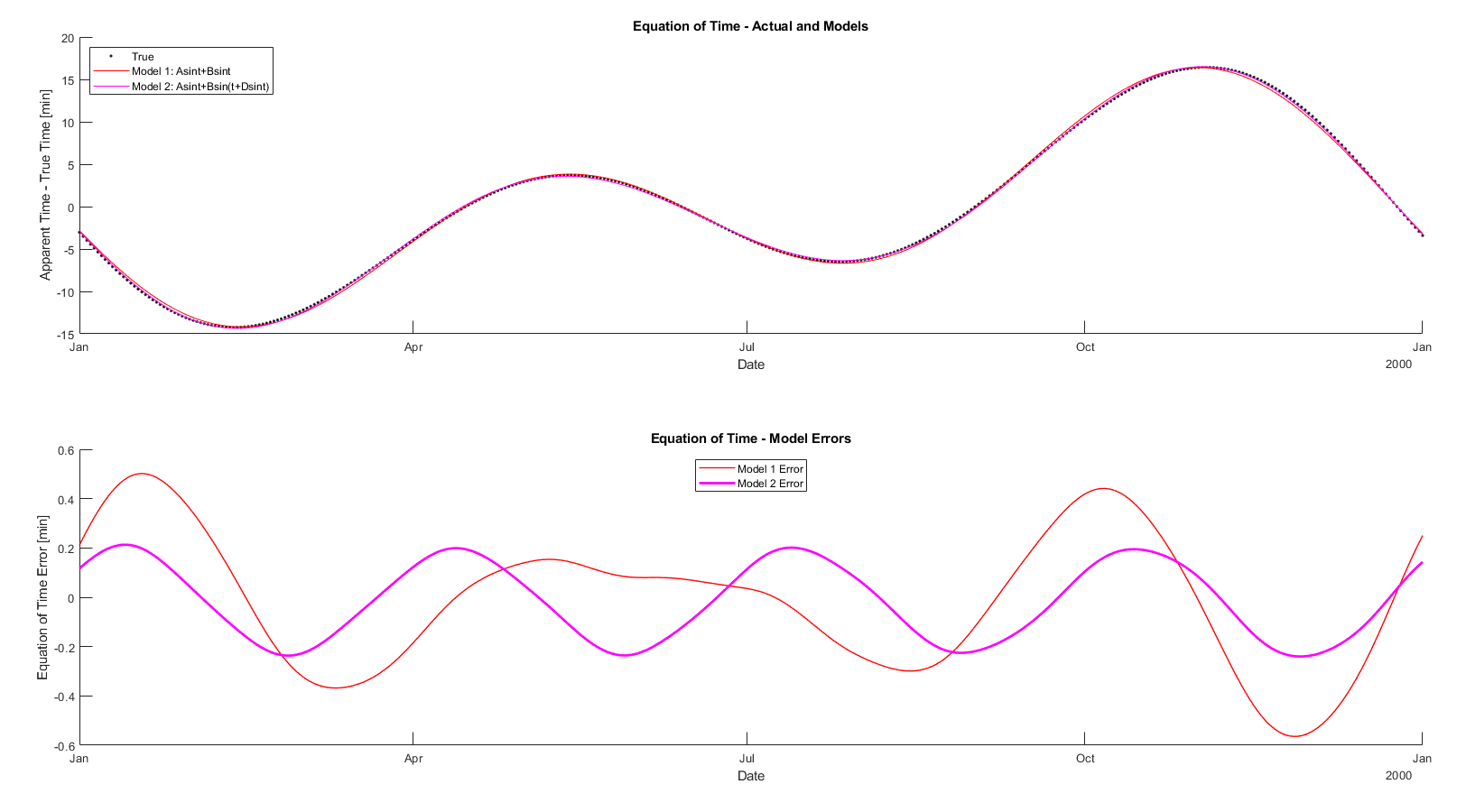
If that’s all there is to it then why are we only a third of the way through this article? Well, it turns out that when you compare the output of this function to the actual Equation of Time there is still an error that is significant and clearly structured. So what is going on here?
Second Order Model: Coupling
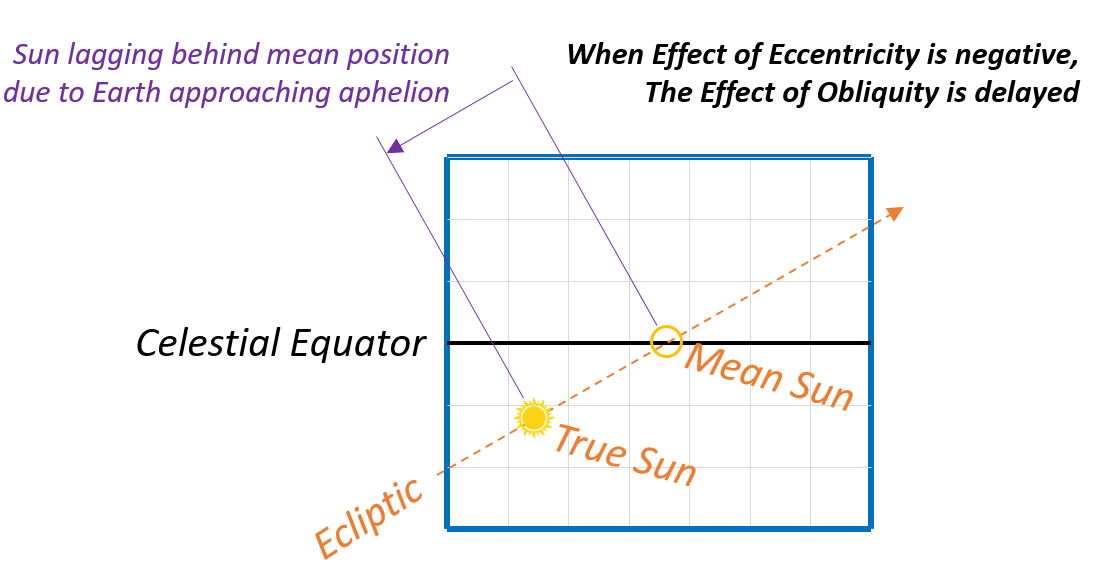
The first effect that we need to compensate for is that of coupling, specifically the effect of eccentricity on obliquity. As convenient as it is to consider these two effects as independent they are not entirely so. If you look at the image of the effect of obliquity, you can see that it is zero at the solstices and the equinoxes. However this is a tad ambiguous because those terms are used in both time and geometry referenced meanings. The date of the vernal (spring) equinox is in basic terms when the sun crosses the celestial equator in an ascending direction, but due to the sun’s uneven motion (from eccentricity) this crossing could actually occur a bit early or a bit late. In mathematical terms, the eccentricity additionally causes a phase-shift to the obliquity.
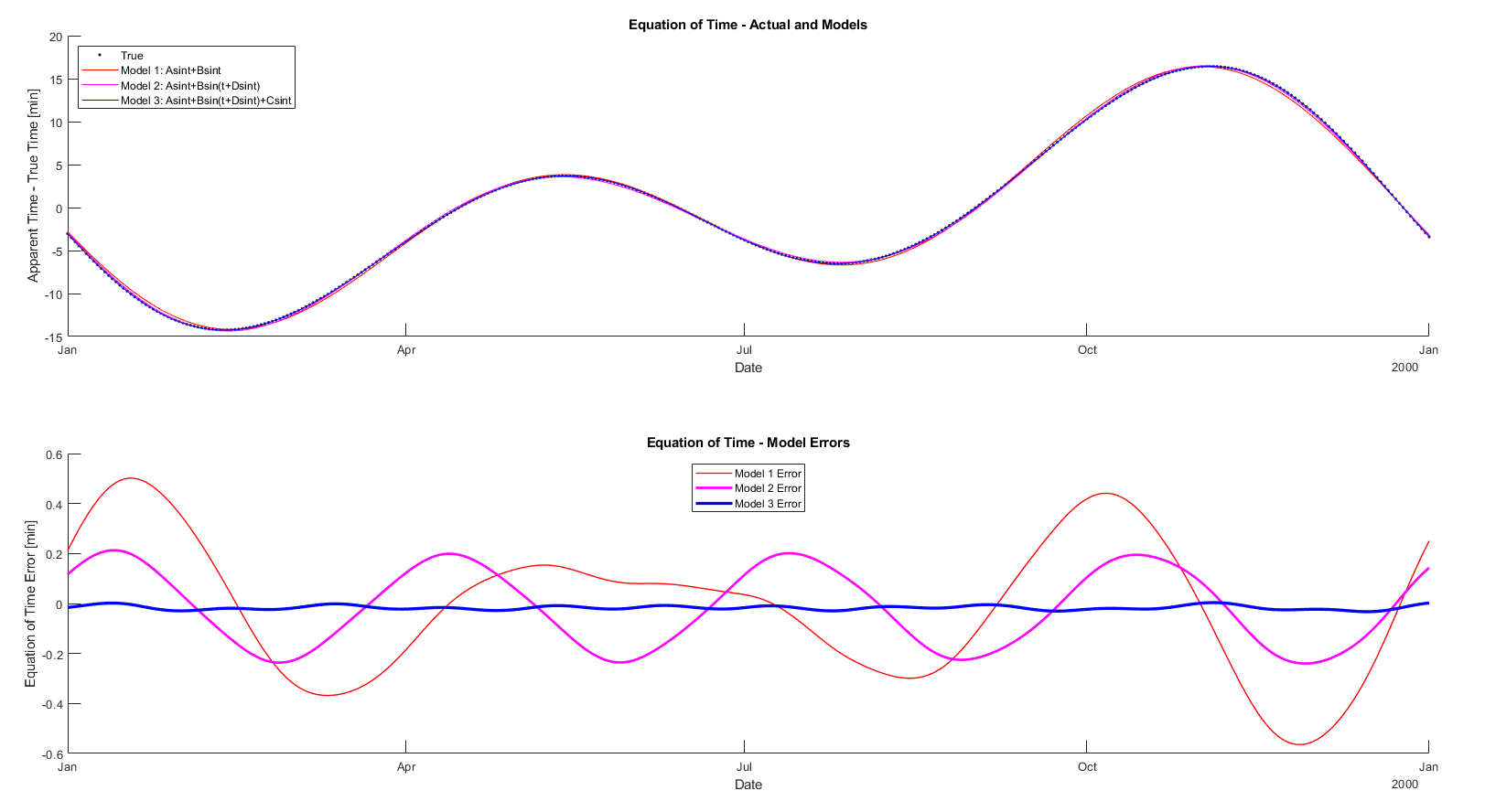
Error Analysis of Second Order Mechanism
When we add the coupling term in the error is about cut in half but more importantly the weird May hump is eliminated and the residual error has very clear structure to it, so we know that we’ll be able to further reduce it.
Mechanisms For Emulating a Second Order Model
There are only a few clocks in the world that model this directly, of note are the Strasbourg Cathedral Clock and the Jens Olsen World Clock. Let’s take a look at each of them accomplish it.
Strasbourg Cathedral Clock
This famous clock uses a pair of stacked face cams to linearly sum the effects of eccentricity and obliquity. The eccentricity cam is at the bottom and rotates at a fixed height once per anomalistic year. It lifts and lowers the entire obliquity cam assembly, which has its own output being lifted and lowered by a cam. In this fashion the height of the two cams are added together at any given time. However the genius portion of this design is that while the lower eccentricity cam is driven by a conventional spur gear, the upper obliquity cam is driven by a helical gear. The purpose being that when the effect of eccentricity is high (and thus the obliquity cam assembly is lifted up) the angle of the helix causes the obliquity cam to be rotated slightly ahead. And of course the converse is true as well. A more drastic angle yields more coupling, while an angle of zero (so a spur gear) would yield none.
Jens Olsen World Clock
The Jens Olsen World Clock in Copenhagen uses a completely different approach in the basic assembly, as well as how the coupling is captured. The yearly eccentricity and biyearly obliquity rates are established by independent gear trains but both culminate in a Tusi Couple which creates a pure sinusoidal linear signal via steel ribbons. The ribbons motions are added via a pulley that is connected to the dial. Between the obliquity gearing and its corresponding Tusi Couple there is a differential which acts like a rotational adder between the gearing itself (most of the motion) and the coupling term from the eccentricity gearing. This is accomplished by having the differential frame attached to a small eccentric on the eccentricity arbor, which rocks the differentially to add the coupling signal.
Third Error Model: Harmonics (i.e. ‘twere never sinusoids!)
I alluded to the fact that we could further reduce the error and there was clearly structure for further reduction in the residual error of the second order model. The residual has a very clear period of 1/4 of a year, so we can add another sinusoidal term to it and we get a drastic reduction. But…what is this mystery third signal and why does it look like there is now a tiny 1/12 year period still left? The short answer is that we have been using sinusoids to model periodic functions that are NOT sinusoidal.
True Form of Eccentricity Term
If we artificially increase the eccentricity of the Earth to a much higher value for effect and look at the error function formed it is clearly not a sinusoid. So let’s just find the equation for that function and use it instead of a sinusoid right? Well, minor problem on that front because this function comes from Kepler’s Equation and it is transcendental (has no algebraic solution).
The best we can do is use a series expansion to model it, which is shown on the right. ν is the true anomaly (actual position) and M is the mean anomaly (average position) so the effect of eccentricity is ν-M. The first line of the expansion is sinM, with a period of 1 year and an amplitude that works out to 7.66 minutes. This is the piece that we’ve been using so far. The next term has a period of 1/2 an anomalistic year and a magnitude of 4.8 seconds, this one is a little tricky because it will be heavily overlapped with the obliquity term of 1/2 a tropical year. Beyond that the amplitude of the 1/3 and 1/4 anomalistic year terms drastically drops to 0.07 sec and 0.001 sec, respectively. An infinite sum like this can be represented either with encoded geometry like a cam, or by mechanically summing a finite number of mechanical motions (truncated at a reasonable limit). To this effect the Strasbourg Cathedral Clock design is superior to Jens Olsen’s since the eccentricity cam can be shaped to include any number of terms, in contrast to a Tusi Couple that is stuck being sinusoidal.
True Form of Obliquity Term
A similar situation exists with the obliquity term, but while it is not a simple sinusoid it does thankfully have an algebraic solution. The equation for the Right Ascension of the sun traveling along an inclined plane like the ecliptic is shown below. At a zero tilt angle the angle along the ecliptic and the angle along are the same, but as the tilt angle is increased there emerges a difference between the two. For low angles this appears very similar to a sine wave, but becomes visibly different at higher tilt angles. For our modest axial tilt of 23.4° (and thus 23.4° tilt of the ecliptic relative to the celestial equator) the error of using a sine wave is about 12 seconds. This corresponds to the second harmonic of the obliquity and is the primary residual error we were seeing with sine waves for both effect.
Who Cares Why, if It Is Repeatable Just Encode It in a Cam!
The Limitations of Cams: Precession
Both effects that contribute to the Equation of Time are subject to precession (slow drifting of otherwise static orbital elements. The effect of eccentricity is zero at perihelion, thus as the argument of periapsis changing (apsidal precession) slowly moves the timing of this effect with a period of approximately 112,000 years. The effect of obliquity comes from the axial tilt of the earth and thus is affected by axial precession with a period of approximately 26,000 years. This is also referred to as the precession of the equinoxes. In the animation below the year 2000 Equation of Time is shown for reference as the true Equation of Time advances 10,000 years. After that time, it looks completely different!
This is a common approach actually and is generally appropriate, especially for small assemblies like watches of simpler clocks for which space is at a premium and the accuracy is already limited by the size of the dial. This approach, shown on the right, results in an oblong radial cam often called a kidney cam due to the shape. It is rarely the actual Equation of Time in polar coordinates, due to the arc through which the follower travels. It can be mathematically solved for but is more traditionally sketched out by hand. This allows for a theoretically exact form of the equation for a given year, however it has no way of compensating for the EoT changing over the years.
With a yearly cam system shown above, the two effects shifting relative to each other cannot be captured. The drift may seem to be happening on long periods of time, but even across a human lifetime the shift could be 45 seconds. For things like cathedral clocks that are multigenerational the error that results is unacceptable. The accommodation for this is a more specific understanding of what constitutes a year, the terms anomalistic year and tropical year have been sprinkled throughout this article but now it is time for them to really shine. The difference between the various types of year are all about from what it is referenced.
A sidereal year is the simplest, it uses a true inertial frame and is 365.2564 days long.
An anomalistic year is the time for the earth to go from perihelion to perihelion, because that is a moving reference due to apsidal precession that is 365.2596 days. Since the effect of eccentricity is zeroed at perigee, using this period compensates for this precession.
A tropical year is the time for the earth to go from equinox to the same equinox, due to axial precession that is 365.2422 days. Since the effect of obliquity is zeroed at the equinox, using this period compensates for this precession.
Both the Strasbourg Cathedral Clock and the Jens Olsen World Clock distinguish between anomalistic and tropical years, although only the former has the ability to capture the non-sinusoidal waveforms of both effects. There is, however, one other clock that has a novel way of capturing both effects in a single cam in full accuracy. The Clock of the Long Now uses a 3-dimensional cam, with the linear dimension corresponding to 12,000 year period. The follower moves across its length in that time, while the cam rotates very close to once per tropical year, tracing an extremely dense spiral. The two precession rates are visible as twisting in an unusually organic shape.