When are Sunrise and Sunset?

By Spencer Connor

It SEEMS like a simple question but it is actually a fairly complex thing to determine. Most of us are aware that the longer days of summer and shorter days of winter mean that the time of sunrise and sunset vary throughout the year, but how many know how it varies to be able to predict it? I certainly didn’t for most of my life, and you can too! There are two ways to look at the problem geometrically and both are correct, I’m going to provide visuals primarily from the observer point-of-view rather than the solar system point-of-view since I find it a bit more intuitive.

A couple brief clerical notes:

I will be discussing this topic using a northern hemispheric reference, the concept is identical (although mirrored) in the southern hemisphere.
Sunrise and sunset are analogous in the sense that they are symmetrical about the solar meridian. I switch between them in the article, but

Let’s start with the image on the right, where we can imagine ourselves standing under the celestial sphere sky at some northern mid-latitude like the central Europe. The celestial north pole is somewhere between the northern horizon and overhead, and the celestial equator goes from pure East and pure West across the southern sky. The celestial sphere rotates once per day, carrying the stars and sun as a largely fixed pattern overhead. Over the year the sun travels on an inclined circle, the ecliptic, crossing the celestial equator twice and wandering as far as 23.4° off of it in both directions. The crossings are called the equinoxes, and the 23.4° maximums the solstices. The summer solstice is the maximum to the north (in the northern hemisphere) and the winter solstice is the maximum to the south (in the northern hemisphere).

On the Equinoxes

The sun is on the celestial equator, rising directly east and setting directly west at a time of year with equal length of day and night. They occur as 6am and 6pm local solar time, although not exactly 6am/6pm mean time due to the Equation of Time.

On the Summer Solstice

The sun is off of the celestial equator by 23.4° towards the north pole (called a declination of +23.4°). At 6am local solar time the sun is directly east (and directly west at 6pm LST) but is already above the horizon so there is an additional portion of time that is daylight when the sun is farther north.

On the Winter Soltice

The sun is off of the celestial equator by 23.4° away from the north pole (called a declination of -23.4°). At 6am local solar time the sun is directly east (and directly west at 6pm LST) but is still below the horizon so there is an additional portion of time that is darkness and the sun rises/sets farther south.

Getting Into the Numbers

Now I took the liberty of labeling the latitude in those images to make an effect clear: the degree to which the days vary in length throughout the year depends on the latitude. At low latitudes the sun rises close to straight off of the horizon and whether it is to the north or south a bit doesn’t change the duration of the day much. But at higher latitudes where the sun traverses at a shallow angle the difference becomes substantial. In fact at some high values of latitude (<66.5°) the effect is so substantial that sunrise and sunset meet at midday and midnight and there are periods of year with entire days of daylight or darkness.

A contour plot of the hours of daylight as a function of latitude and day of the year. Credit: Sebastian Helm

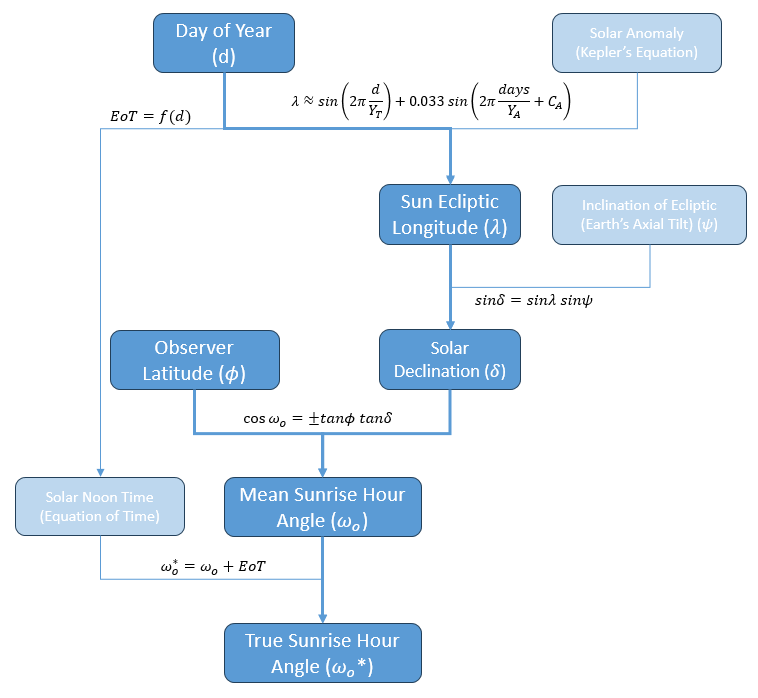
In the image on the right this effect can be seen in the Arctic and Antarctic Circles. If we do the spherical trig to calculate this effect we end up with what is called the Sunrise Equation:

Where:

ω∘ is the solar hour angle* at sunrise/sunset.
ϕ is the latitude
δ is the solar declination (the ±23.4° variation previously discussed)

*you can think of solar hour angle as the portion of daylight. At the equinox sunrise and sunset are at ±90° so there is 180° of light and 180° of darkness

Mathematically, the inverse cosine is undefined for inputs outside of [-1,+1], which this equation violates when tan(ϕ)>tan(90-δ). This corresponds to the arctic/antarctic circles.

Is a Sine Function Close Enough?

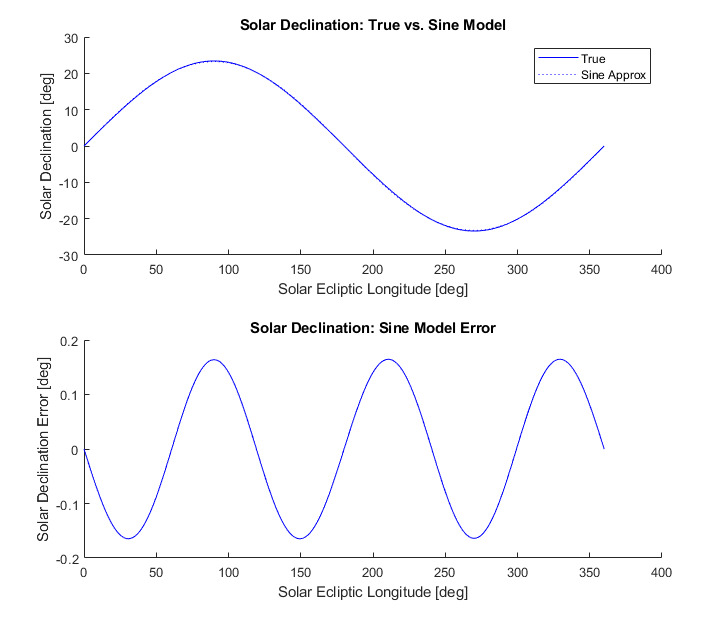
For some latitudes the variation in daylight coming from varying sunrise/sunset times is small enough that you can approximate it with a sine function. For example, the Jens Olsen World Clock uses a scotch yoke sinusoidal function generator for this purpose. Practically, it is almost always sufficient, but the accuracy degrades quickly as the latitude increases. In the figure on the right we can see that at 60° latitude there is more than 45 minutes of error in the fall. For the best astronomical clocks this is unacceptable, and a more complex model (i.e. the actual sunrise equation) should be used. To do so we’ll need to figure out how to get that solar declination value….

Solar Declination

So how does this actually change as the sun travels along the ecliptic? We know that it crosses the celestial equator at the equinoxes and varies an equal magnitude in both directions between them, and this one looks even closer to a sine function than the sunrise equation. But it is not exactly, it takes the form of the equation below and there is still a third harmonic error in the sunrise estimation if a sine function is used here (as seen in figure on right).

Where:

δ is the solar declination
λ is the solar ecliptic longitude
ψ is the inclination of the ecliptic: 23.4°

Note for attentive readers I’m using solar ecliptic longitude here instead of time of year, we’ve glossed over the equation of time a bit since that isn’t the focus of this article but you can read about it here.

Uhh okay, but then how do we calculate ecliptic longitude?

Ecliptic Longitude of the Sun

The ecliptic longitude is just where along the ecliptic the sun is at that time of year (with the vernal equinox crossing point as zero). For the most part the sun moves pretty evenly in the sky throughout the year, in fact this is because earth is moving at a fairly uniform speed around the sun thanks to its low eccentricity orbit (close to circular). But it’s not perfectly circular, the result being that the earth is moving slightly faster or slower at different times of year and from the point-of-view of an earthling that makes the sun appear to slightly speed up or slow down. This is known as the solar anomaly (or more generally the equation of the center) and you can read more about it on the page about the equation of time (the effect of eccentricity). Suffice to say there is a small correction to make, and it’s going to have to be an approximation given that it’s a transcendental function. A reasonable function to use would be:

Where:

λ is the solar ecliptic longitude
d is the days since the vernal equinox
YT is the duration of a tropical year in days, 365.2422
YA is the duration of an anomalistic year in days, 365.2596
CA is the day offset from the vernal equinox to perihelion (about 76 days)

Note that we are now distinguishing between tropical years (that have been assumed thus far) and anomalistic years, which are referenced from perihelion rather than the equinox. The difference can generally be considered a static offset, unless accuracy is needed on the scale of hundreds of years. The equinox precesses with a period of about 26,000 years and Earth’s apsides precess with a period of 112,000 years, so generally there is not a pressing need to distinguish between them.

Final Answer (for the Theory at least)

Modeling Sunrise and Sunset Mechanically

If you’re only interested in the theory this is your stop to go about your day, but for those mechanically minded like myself this is where the fun really begins. How do we come up with a mechanism, really an analog mechanical computer at this point, to calculate sunrise time for something like an astronomical clock?

There are a couple high-level approaches here:

Look at the end product and simply transcribe the function into a cam that repeats on a regular basis. This is generally the easiest and most practical design, but beyond the radial variable (here the time of year) there is no way to adjust anything else. For example it will only work for a single latitude and can not compensate for orbital precessions.
Create a series of serial mechanisms that each emulate a function in the map below. This is far more complicated but yields a theoretically perfect output that can be adjusted.

#1 requires no substantial design thought so we’re just going to look at #2 here, and will assume as inputs we can have mean rotation rates at any rate necessary supplied by the gearwork.

We can do this in a series of distinct steps:

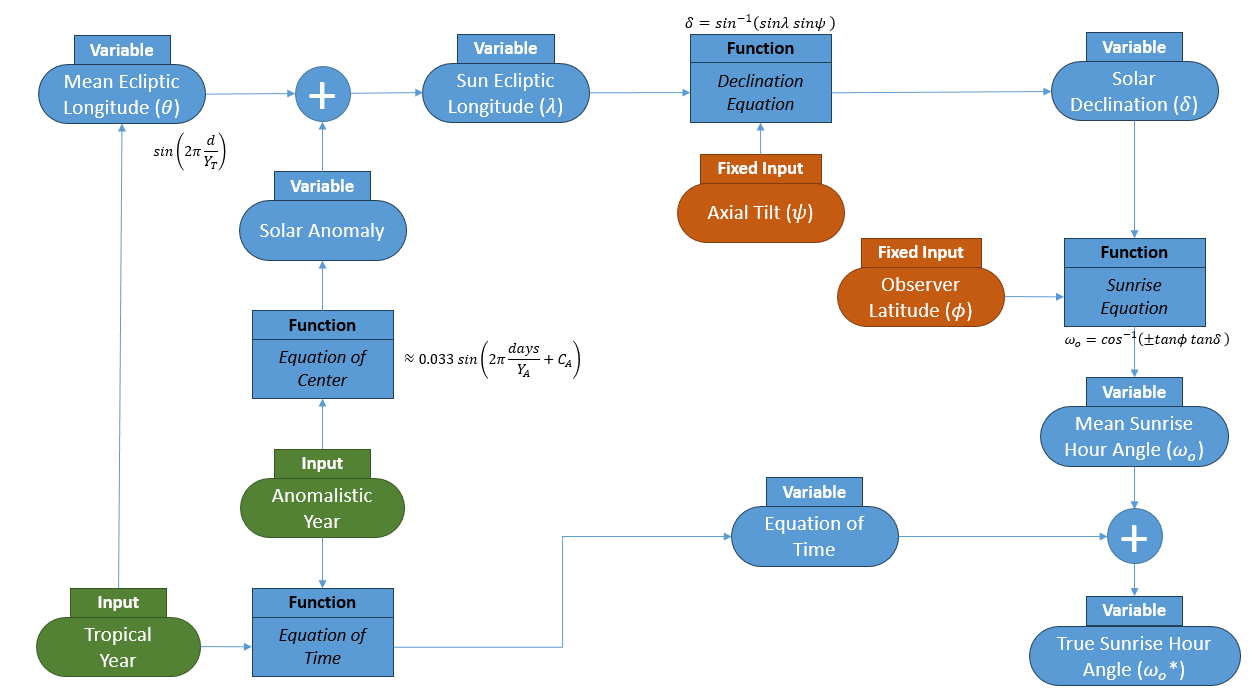
Step 1: Map Variables and Functions

We can map out all the variables and equations as a function of the two input variables: time of tropical year and time of anomalistic year, and two fixed inputs: axial tilt and latitude.

Step 2: Decompose into Individual Functions

We can then break the map down into the simplest arithmetic functions, which results in four unique trigonometric functions, addition, scalar multiplication, and the equation of time function. As has been mentioned previously, the equation of time is a complex function deserving of its own explanation and mechanism so we’ll assume that it’s generated on its own.

Step 3: Identify Mechanisms for Each Basic Function

We’ll next need to identify a mechanism for each simple function.

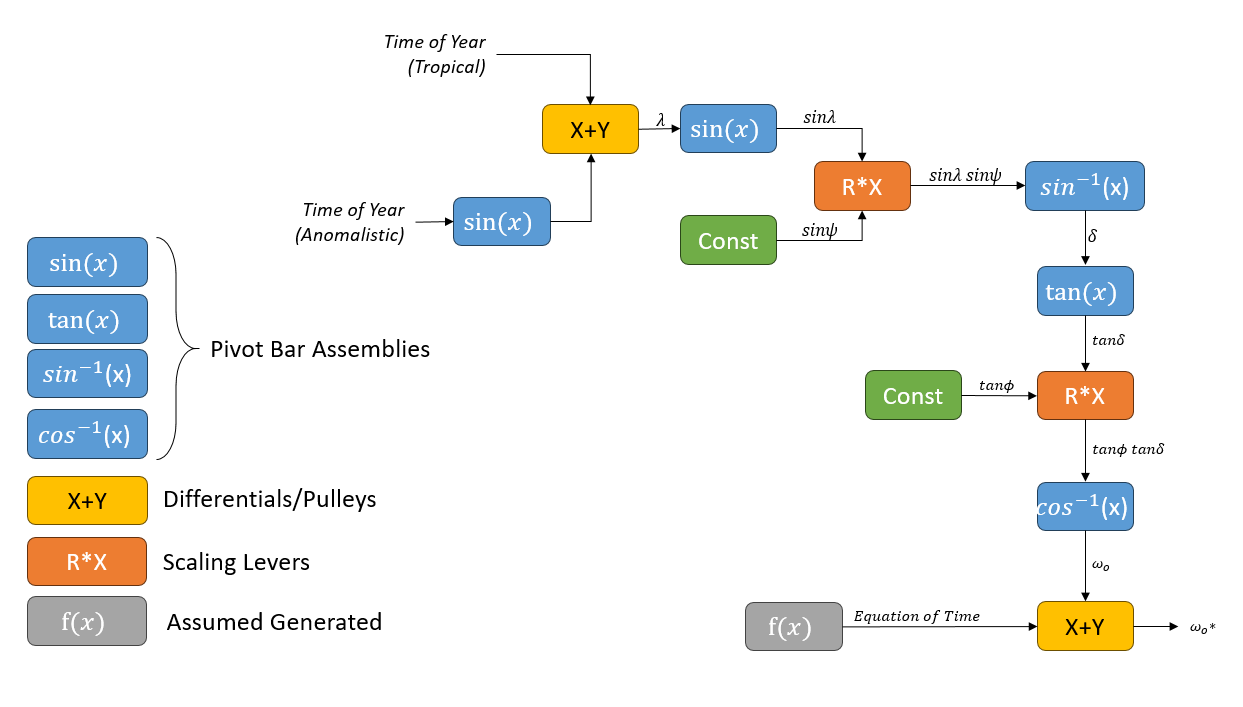
Trigonometric functions tend to be a sector and pivot bar since they involve an angle and a distance.
Addition can be done with a differential if the rotation is unbounded. If not, it is more easily accomplished with summing pulleys or whipple trees
Scalar multiplication can take many forms but usually ends up absorbed into an adjacent mechanism. For now we’ll assume ratio pulleys

Below are the mechanisms I selected for the required simple functions, but there are alternative available for all of them.

Step 4: Replace Functions with Mechanisms and Link Together

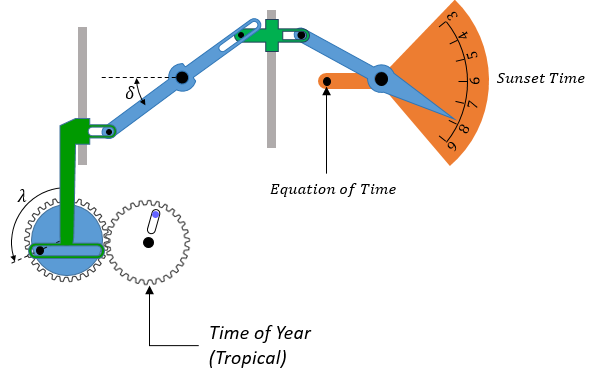
Now we’ll splice each of the simple mechanisms in and link them together. Variables can be either rotational or translational, and you may need to pick mechanisms that are conducive to one or the other or add a simple translator like a sector. At this point we’re just getting everything in, so don’t worry that it looks rather complicated.

Step 5: Simplify

Now we boil down that complex mess to the simplest version. There are many ways to do this and not really an overarching approach, so I’ll simply list the specific alterations that I made and on what basis:

Both sector translators were removed, as I am confident that the end result will have some ways to emulate the same multiplication
The two declination arms center top are always at the same angle so combined that into a single arm.
With the right sector translator removed there are two sliders (center and right) now that move together, so combine those into a single one.
The summing with equation of time at the end was removed, in favor of a dial moving in the inverted direction relative to the needle. I like this approach generally, because you can show the sunrise in mean time on the moving dial and in solar time on a second fixed dial.

None of these alterations affect the theoretical accuracy of the device, but there is an additional one I added that does:

Replaced the input differential and scotch yoke from the anomalistic year with an Antikythera-style pin slot pulser. Once the offset is set on this assembly it will drift at a rate of 1 deg per 72 years. For this application this has been deemed acceptable for the reduction in complexity.

Step 6: Solve for Fixed Geometry

Finally, we need to solve for the fixed geometry to determine what it should be. In our end result (outside of the pin-slot anomaly assembly) there are 4 fixed distances. When solved on the right we find that two will be determined based on the axial tilt of the earth, and two will be determined based on the latitude of the observer. It is very common for this to be the case, as intuitively we should be able to scale the design to whatever overall size we desire and still produce quantities like angles correctly. A final thought is to consider if any of these would want to be manually adjustable. In this case the axial tilt of the earth is not changing soon, but perhaps having latitude be adjustable is useful. As a ratio between b and c, this could be accomplished by translating the central vertical slide bar left and right.

Step 7: Verify and Optimize

Wait, why is there still error? There is a noticeable offset still after accounting for all of those variables! That’s due to the variable we DIDN’T account for:

Atmospheric Refraction. The atmosphere will bend sunlight around the earth such that when we see the sun start to set it is actually fully below the horizon. The amount of bending depends on local temperature and pressure, but is generally around 0.83° which corresponds to seeing sunset ~6 minutes after the sun center is below the horizon. However, since the sun is setting at different angles throughout the year, this time is slightly variable (being longer at midsummer and midwinter when the sun is setting farther from vertical).
Center vs. Limb Set. The sunrise equation gives the hour angle when the center of the sun is at the horizon but generally sunset is considered when the upper limb of the sun passes below the horizon, a difference of one solar radius. This would again be a static offset of about 1 minute except for variability in the angle of sunset similar to #1 above, and variation in the apparent size of the sun (larger at perihelion in January, thus longer to traverse the horizon).

This is about the point when we decide if we want to incorporate these additional terms in earnest. I decide not to, given that a simple offset will get the residual error to about ±1 min and that is far below other uncontrollable factors like horizon terrain. So the final answer for this study (configured for 40 N°) is below: